Los números de Fermat son aquellos que se escriben de la forma
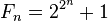
Fermat conjeturó, más bien afirmó aunque no se molestó en comprobar, que todo eran primos, ya que
- F0=3
- F1=5
- F2=7
- F3=257
- F4=65537
eran primos. Pero erró, el único de sus errores en las múltiples conjeturas que realizó. Tenía por costumbre dar afirmaciones sin proporcionar la demostración.
Fue Euler quién probó que F5 no es primo y que podía factorizarse en
F5=4294 967297 = 641* 6 700417
A partir de aquí hubo una carrera por determinar quién era el siguiente primo en los números de Fermat. Y todavía no se ha encontrado.
Esta carrera ha llevado pareja la de factorizar los Fn compuesto, tarea menos compleja que determinar si son primos, pero pero muy costosa ante la magnitud de los números. Por suerte para los cazadores de factores, cualquier divisor primo de Fn tiene que ser de la forma k·2n+2 + 1, con k entero positivo. Así que, a calcular.
En mathpuzzle.com he encontrado el último factor calculado, a fecha del 15 de marzo de este año:
81909357657279 · 254 + 1 factor de F52, hallado por Cedric Vonck.
Una de las aplicaciones más importantes de estos primos de Fermat es un resultado que obtuvo Gauss: Un polígono regular de n lados puede construirse con regla y compás si n es igual a una potencia de 2 o al producto de una potencia de 2 por primos de Fermat distintos entre sí.
Un ejercicio muy bonito es probar que todos los números de Fermat a partir de n>1 terminan en 7. ¿Quién se anima?