Un paseo por los coeficientes binomiales

Cuando tratamos en probabilidad los números combinatorios, estamos hablando de las  formas en que se puede extraer subconjuntos a partir de un conjunto dado. También los llamamos coeficientes binomiales,  que nos aparecen en el famoso triángulo de Pascal.

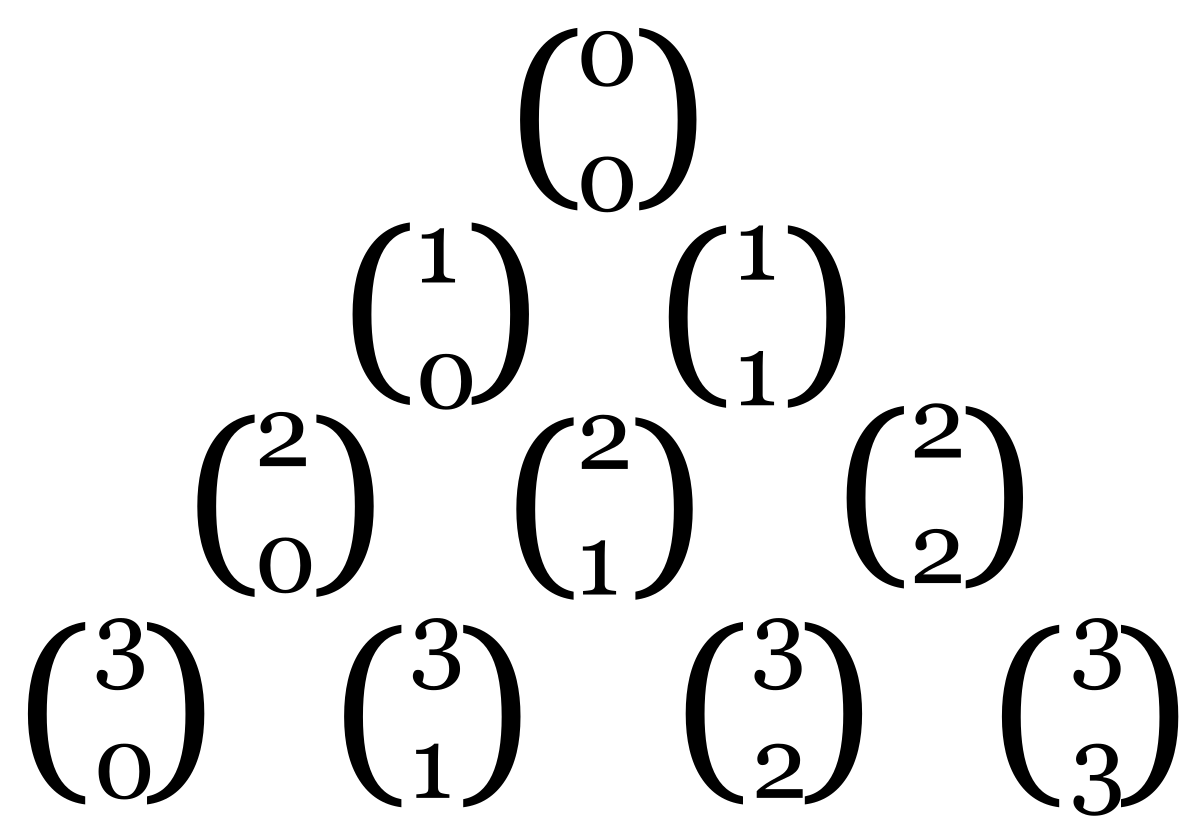
Esta concepción define el coeficiente binomial de dos números enteros $n,k>0$ como
$${\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}}$$

Hasta aquí lo que normalmente vemos. Pero, ¿podemos hacer el número binomial siguiente?:
$${\displaystyle {-4 \choose 3}}.$$
Para resolver el problema necesitamos herramientas nuevas. Sabemos que el número combinatorio también puede escribirse como
$${\displaystyle {n \choose k}={\frac {n(n-1)\ldots (n-k+1)}{k!}}}.$$
Definamos, para cualquier real, $x\in\mathbb{R}$, y $k\in\mathbb{Z}^+$,
$$(x)_0=1$$
y
$$(x)_k=x(x-1)\ldots(x-k+1),\, k>0.$$
Entonces,
$${\displaystyle {x \choose k}={\frac {(x)_k}{k!}}}.$$
Ahora,
$${-4 \choose 3}=\frac{-4(-4-1)(-4-2)}{3!}=-\frac{4·5·6}{6}=-20.$$
Del mismo modo
$${1/2 \choose 3}=\frac{\tfrac{1}{2}\left(\tfrac{1}{2}-1\right)\left(\tfrac{1}{2}-2\right)}{3!}=\frac{1}{16}.$$
Parece ridículo, porque no podemos interpretarlo como al principio. Pero esto no es óbice para dar una definición que, algún día, tenga interpretación.

Generalizemos aún más. Conocemos la relación de los factoriales con la función gamma: $\Gamma(n+1)=n!$ para todo $n$ natural. Entonces
$${\displaystyle {n \choose k}={\frac {\Gamma(n+1)}{\Gamma(k+1)\Gamma(n-k+1)}}}.$$
Apliquémoslo a números reales $x,y$:
$${\displaystyle {x \choose y}={\frac {\Gamma(x+1)}{\Gamma(y+1)\Gamma(x-y+1)}}}.$$
Es más, la función Gamma nos lleva a un resultado curioso:
$${x \choose y}\cdot {y \choose x}={\frac {\sin((x-y)\pi)}{(x-y)\pi}}.$$
¿Y lo podemos hacer más complejo? Sí. Para cualesquiera $z,w\in\mathbb{C}$ definimos el coeficiente binomial ${z \choose w}$ como
$${\displaystyle {z \choose w}=\lim_{u\to z}\lim_{v\to w}{\frac {\Gamma(u+1)}{\Gamma(v+1)\Gamma(u-v+1)}}}.$$
Con las definiciones escritas vemos que
$${1 \choose \tfrac{1}{2}}={\frac {\Gamma(1+1)}{\Gamma(\tfrac{1}{2}+1)\Gamma(1-\tfrac{1}{2}+1)}}=\frac{4}{\pi};\quad {\tfrac{1}{2} \choose 1}=\frac{1}{2}.$$

Esta entrada participa en la Edición 8.4 “Matemáticas de todos y para todos” del Carnaval de Matemáticas cuyo anfitrión es, en esta ocasión, matematicascercanas