La cuadratura de la lúnula

Una lúnula es una figura con forma de luna creciente obtenida mediante la intersección de dos círculos. En realidad, esta intersección generaría dos lúnulas. Si lo vemos desde la geometría plana es el área cóncava limitada por dos arcos. La convexa es a la que denominamos lente.

Lúnula proviene del latín lunŭla. Sin embargo de ellas comenzaron a hablar los griegos. En concreto nos interesa Hipócretes de Quíos, quien puso interés en ellas debido a que encontró una manera de cuadrar su área.

Para los griegos la cuadratura de las figuras supuso un paso ambicioso en las consideraciones de las proporciones: todo era reducible a una proporción. Pero el mundo se les derrumbó cuando se toparon con los números inconmensurables.

Este cisma se concretó en el problema de la cuadratura del círculo: ¿es posible relacionar un círculo y un cuadrado de igual área?, utilizando regla y compás. Este problema griego se conoció como el Problema de la cuadratura del círculo, y expresaba la dificultad de los griegos de entender los números más allá de los racionales.

El problema se ha convertido en la metáfora de un imposible, y así lo utilizamos, sin matizar la coletilla matemática: con regla y compás. Véase la ilustración de este problema, con y sin coletilla matemática, que nos expone gaussianos en ¿Quién dijo que la cuadratura del círculo era imposible?.

Sin embargo, los griegos intentaron resolverlo mediante la geometría euclídea, llegando a conclusiones que rozaban el éxito. Ese convencimiento de que nada era imposible, apareció con Hipócrates de Quíos. Este quionio demostró que el área de la lúnula es la cuarta parte del cuadrado inscrito, que se corresponde con un triángulo.

La cuadratura del triángulo era conocida (Cuadratura de un triángulo cualquiera), en consecuencia la cuadratura del círculo se conseguiría.

El éxito casi se consigue, pero falla. Bastantes siglos después el gran matemático persa Alhacén(945-1040) comprobó que era posible cuadrar el área de la lúnula:

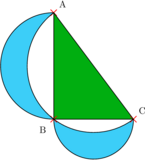
Este trabajo aparece con frecuencia otorgado a Leonardo da Vinci. Es verdad que el polímata florentino sintió curiosidad por las lúnulas y concibió varias cuadraturas mecánicas, en la que posiblemente dedujese las lúnulas de Alhacén. O simplemente conoció los trabajos del musulmán, igual que leyó los trabajos de Vitruvio, para dibujar el Hombre de Vitruvio. El historiador Carl Boyer nos dice: «A menudo se suele considerar a Leonardo como un matemático, pero su mente inquieta no podía concentrarse en la aritmética, el álgebra o la geometría el tiempo suficiente como para hacer alguna contribución importante«. Sí resulta sumamente curioso lo que nos dejó en el folio 112 recto, del Códice Atlántico, en el margen donde figuran tres líneas escritas: «La noche de San Andrés encontré el final de la cuadratura del círculo; terminada la candela, la noche y el papel donde escribía cuando, la hora cumplida, llegué a la conclusión«[Fernando Bombal. La cuadratura del círculo: Historia de una obsesión. Rev. Real Acad. Ci. Exact. Fis. Nat. (Esp) Vol.105, Nº2(2012),241-258].

Entonces, ¿dónde está el fallo que llevó a creer que el paso de la cuadratura de la lúnula daría la del círculo? La concepción de que toda lúnula es cuadrable. Hipócrates encontró la cuadratura para tres tipos de lúnulas: la que parte de un triángulo isósceles rectángulo, de un trapecio isósceles y pentágono cóncavo. Una extensión de la del triángulo rectángulo es la que obtendría Alhacen. Dos más fueron encontradas en el siglo XIX, que el historiador Dunham atribuye los descubrimientos a Euler en 1771: las obtenidas mediante un hexágono y octógono cóncavo[Brian J. Shelburne, The Five Quadrable (Squarable) Lunes]. Hasta el siglo XX estás eran las únicas lúnulas cuadrables, cuando N. G. Tschebatorew and A. W. Dorodnow probaron, utilizando la teoría de Galois, que no habían más[M. M. Postnikov and Abe Shenitzer, The Problem of Squarable Lunes, http://www.jstor.org/stable/2589121].

A veces unos pocos pasos nos hace creer que podemos recorrer todo el camino, cuando es sólo un número de pasos finitos en la infinitud de las matemáticas. Pero sin el aliciente de esos pasos no avanzaríamos.

Esta entrada participa en la edición 7.5 del Carnaval de Matemáticas, alojado en el blog Series divergentes.